Така ситуація має місце у навчанні: тестування, спрямоване отримання інформації про рівень засвоєння певних знань, умінь і навиків (при професійному навчанні), має точно відбивати рівень освоєння цих навичок і цим давати надійний прогноз ефективності конкретної професійної діяльності.
Розглянемо операційну схему шкалювання, що застосовується під час створення критеріального тесту [15]. Нехай є певний критерійС, заради прогнозування якого психодіагност створює якийсь тестХ.
Для простоти представимоС як дихотомічну змінну з двома значеннями - «1» і «0» (наприклад, надійде випускник школи до вузу чи ні). С=1 означає, що i-тий суб'єкт досяг критерію (потрапив у "високу" групу за критерієм, тобто вступив до вузу), С=0 означає, що i-тий суб'єкт не досяг критерію (потрапив у "низьку" групу, тобто не надійшов).
Потім психолог проводить тест Х на вибірці, що його цікавить, і в результаті кожен індивід (школяр) отримує певний тестовий бал. Після того як для кожного індивіда з вибірки стає відомим значення С (наприклад, поступив чи ні до вузу), психодіагност має у своєму розпорядженні всіх індивідівпо порядку зростання балаі для кожного поділу вихідної шкали сирих тестових балів підраховує з якою ймовірністю (Р) кожен індивід (школяр) може потрапити у "високу" групу за критерієм.
Награфіці 8 проілюстровано розподіл ймовірності P(C =1) залежно від . Очевидно, що крива, представлена награфіці 8, є емпіричною лінією регресії З .
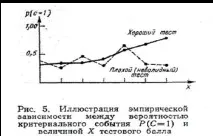
Тепер можна сформулювати основну вимогу до критеріального тесту:лінія регресії має бутимонотонною функцією від Х. Іншими словами, для жодного більш високого значення ймовірність Р не повинна бути меншою, ніж для будь-якого менш високого значення .
Якщо ця умова виконується, то відкривається можливість для критеріального шкалювання сирих балів Х. При критеріальному шкалюванні до поділів сирої шкали Х застосовується поточковий переведення прямо в шкалу Р на підставі емпіричної лінії регресії.
Наприклад, якщо випробуванийА отримав по тестуХ 18 "сирих" окулярів і цьому результату відповідає Р=0,6, то випробуваномуА > ставиться у відповідність показник 60%.
Звичайно, будь-яка емпірична крива є лише наближеною моделлю тієї залежності, яка могла бути відтворена на генеральній сукупності.
Тому зазвичай робляться спроби апроксимувати емпіричну лінію регресії якоюсь функціональною залежністю, що дозволяє потім робити прогноз із застосуванням формули (а не таблиці чи графіка).
Наприклад, якщо лінія регресії має вигляд приблизно такий, який зображений на рис.6, то застосування процентильної нормалізації дозволяє отримати просту лінійну регресіюС за нормалізованою шкалоюZ.
Це якраз той випадок, коли має місце еквівалентність стратегії, яка використовує вибірково-статистичні тестові норми, та стратегії, яка використовує критеріальні норми.
На завершення даного матеріалу, розглянемо операції з аналізу розподілу тестових балів, побудови тестових норм та перевірки їхньої репрезентативності.
Згідно Століну В. В. [15], дії, які послідовно повинен зробити психолог при побудові тестових норм зводяться до такого алгоритму:
1. Сформувати вибірку стандартизації(Випадкову або стратифіковану за яким-небудь параметром) з популяції, на якій передбачається застосовувати тест. Провести на кожному випробуваному з вибірки тест у стислі терміни (щоб усунути іррелевантний розкид, спричинений зовнішніми подіями, що сталися під час обстеження).
2. Здійснити угруповання "сирих" балів з урахуванням вибраного інтервалу квантування (інтервалу рівнозначності). Інтервал визначається величиною W/m, де розмах; m – кількість інтервалів шкали. Необхідно мати на увазі, що угруповання індивідуальних балів, набраних випробуваними по тесту, позначається не тільки на розподілі балів за класами (інтервалами квантування), а й на середніх показниках, що характеризують ту чи іншу властивість, що вимірюється. Експериментальні дані показують [11], що зовсім не байдуже, не тільки те, на скільки класів розбивається вся сукупність отриманих тестових балів, але і як визначаються межі першого класу.
Щоб вийшли адекватніші результати обробки статистичних даних, рекомендується:
-по-перше, не брати надто великий інтервал шкали - він не повинен перевищувати 1/3-1/4 величини середнього квадратичного відхилення;
-по-друге, визначати межі першого класу слід так, щоб мінімальний показник набраних за тестом балів потрапляв приблизно в середину цього класу.
3. Побудувати розподіл частот тестових балів у вигляді таблиці та у вигляді відповідних графіків гістограми та кумуляти.
4. Здійснити розрахунок середнього та стандартного відхилення, а також асиметрії та ексцесу за допомогою комп'ютера. Перевірити гіпотези про значимість асиметрії та ексцесу. Порівняти результати перевірки із візуальним аналізом кривих розподілу.
5. Здійснити перевірку нормальності одного з розподілів (можна за допомогою критерію Колмогорова або з одним із зазначених способів) або провести процентну нормалізацію з переведенням у стандартну шкалу, а також лінійну стандартизацію та порівняти їх результати (з точністю до цілих значень стандартних очок).
6. Якщо збігу не буде - нормальність відкидається, тоді перевірити стійкість розподілу розщепленням вибірки на дві випадкові половини. При збігу нормалізованих балів для половини і цілої вибірки вважати нормалізовану шкалу стійкою.
7. Перевірити однорідність розподілу по відношенню до варіювання заданої популяційної ознаки (стаття, професія тощо) за допомогою критерію Колмогорова. Побудувати графіки гістограми та кумуляти для повної та приватної вибірок. При значних відмінностях розбити вибірку на різноманітні вибірки.
8. Побудувати таблиці процентильних та нормалізованих тестових норм (для кожного інтервалу шкали "сирого" бала). За наявності різнорідних підвиборок для кожної підвибірки має бути своя таблиця.
9. Обговорити конфігурацію отриманих розподілів.
10. У разі негативних результатів - відсутності стійких норм для шкали із заданим числом інтервалів - здійснити обстеження більш широкої вибірки або відмовитися від плану використання цього тесту.
Контрольні питання для самоперевірки: §4, 5. Підрахунок параметрів та оцінка типу розподілу.
1.Что розуміється під поняттям "репрезентативності"?
2. Навіщо необхідна перевірка стійкості розподілу?
3. На чому ґрунтується загальна логіка перевірки стійкості розподілу тестових балів?
4. Як перевіряється репрезентативність критеріальних тестів?
5. Які дії послідовно має зробити психолог під час побудови тестових норм?
Література до теми.
1. Анастазі А. Психологічне тестування. У 2-х кн. М., 1982.
2. Бурлачук Л.Ф., Морозов С.М. Словник-довідник із психодіагностики. - СПб.: Вид-во "Пітер", 1999. - 528 с.
4. Дружинін В.М. Експериментальна психологія: Навчальний посібник – М.: ІНФРА-М, 1997. – 256 с.
5. Загальна психодіагностика/За ред. А. А. Бодалева, Ст Ст Ст..- М., 1987.
6. Основи психодіагностики/За ред. А. Г. Шмельова. Ростов-на-Дону., 1996.
Чи не знайшли те, що шукали? Скористайтеся пошуком:
Вимкніть adBlock! і оновіть сторінку (F5)дуже потрібно
